Computer Science: A Programmer’s Perspective
这个是很久之前的关于csapp中计算机当中数的表示的笔记,图一乐即可
1. A Tour of Computer Systems
Abstractions in Computer Systems
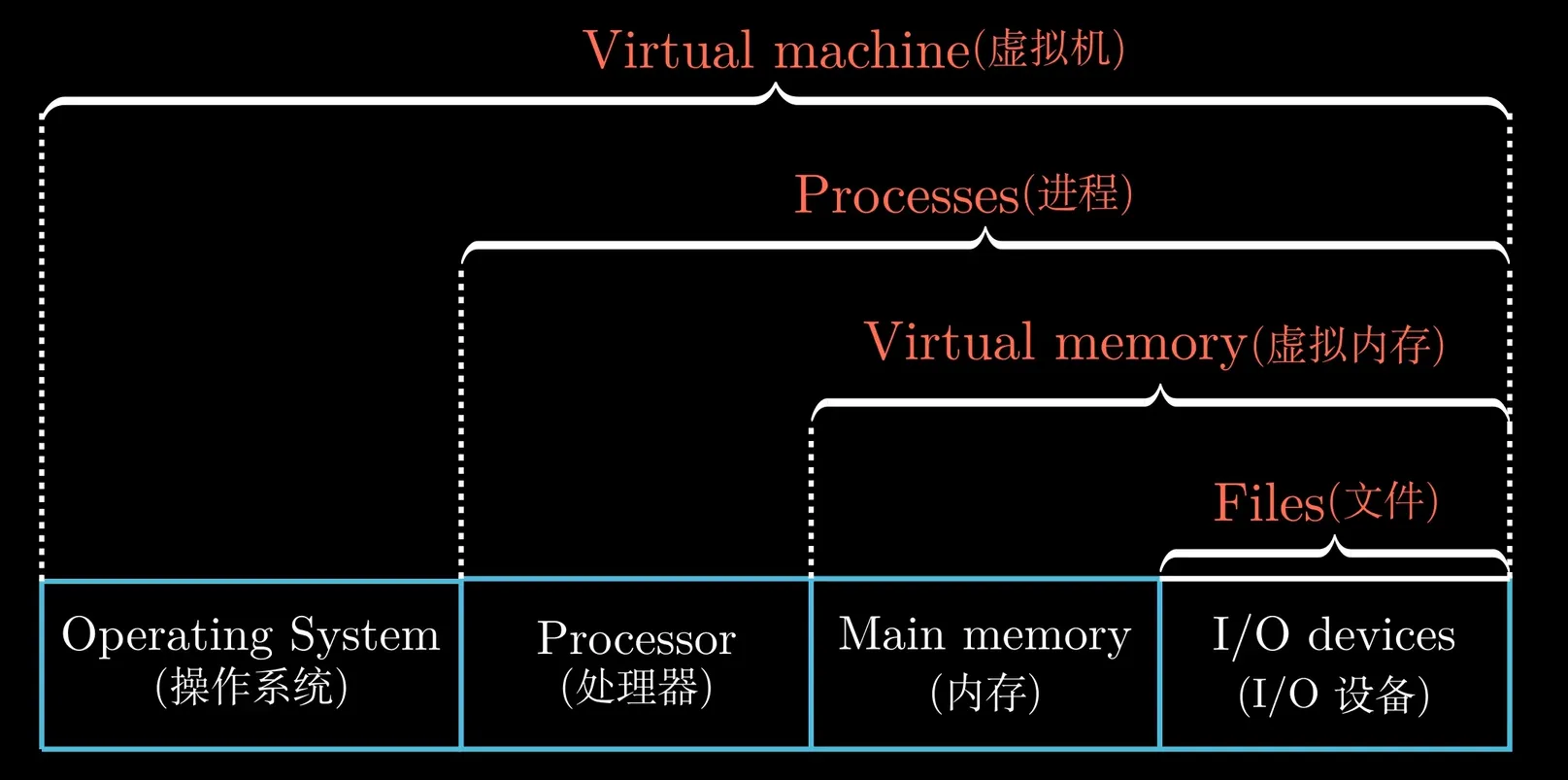
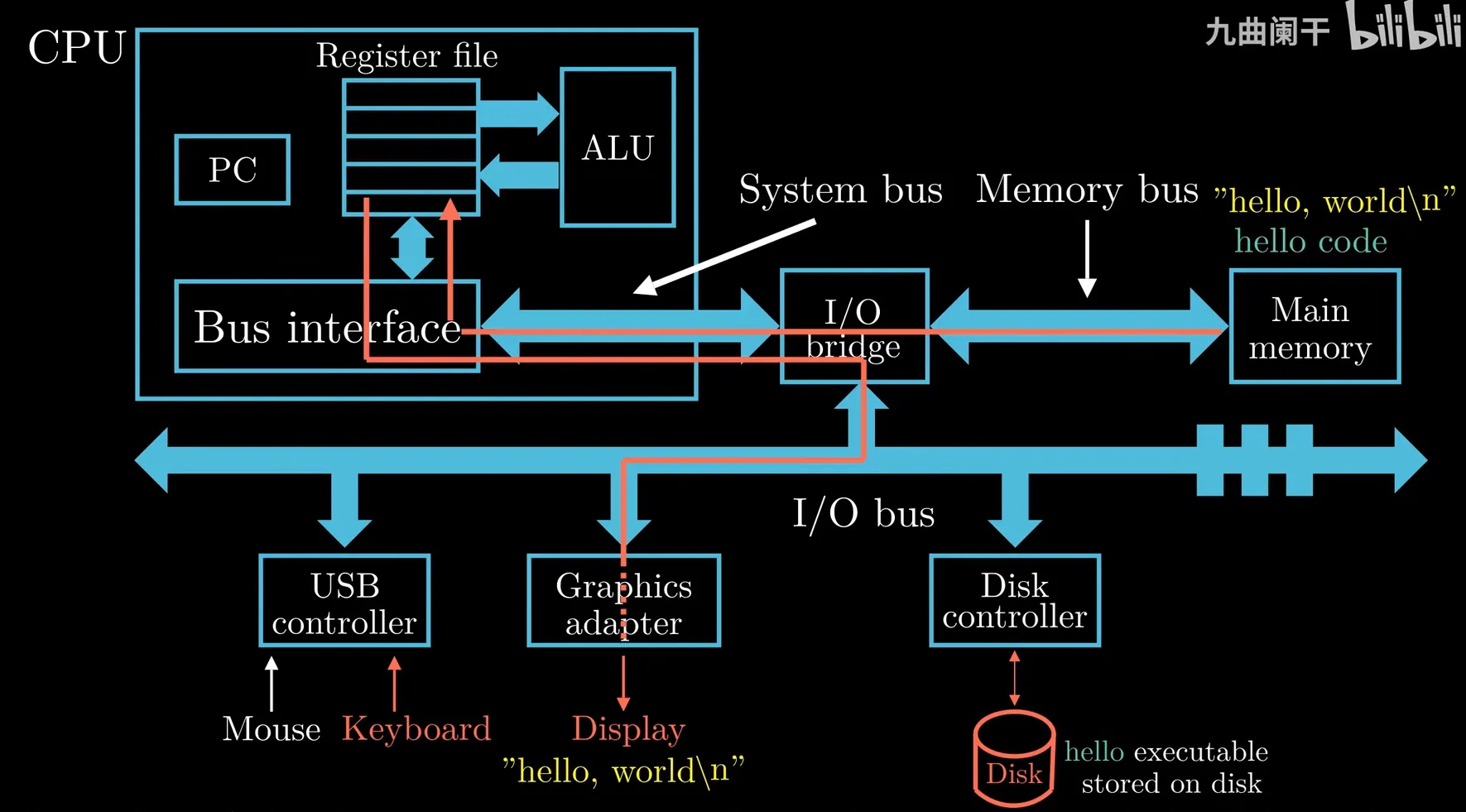
Hardware Organization of a System
- two continuous call may not adjacent
- word: per word, 32bit-machine -> 4Byte, 64bit-machine -> 8Byte
- Program Counter
- Register File(寄存器)
- Algorithm/Logical Unit
- Main Memory(主存)
- Bus(总线)
- I/O devices
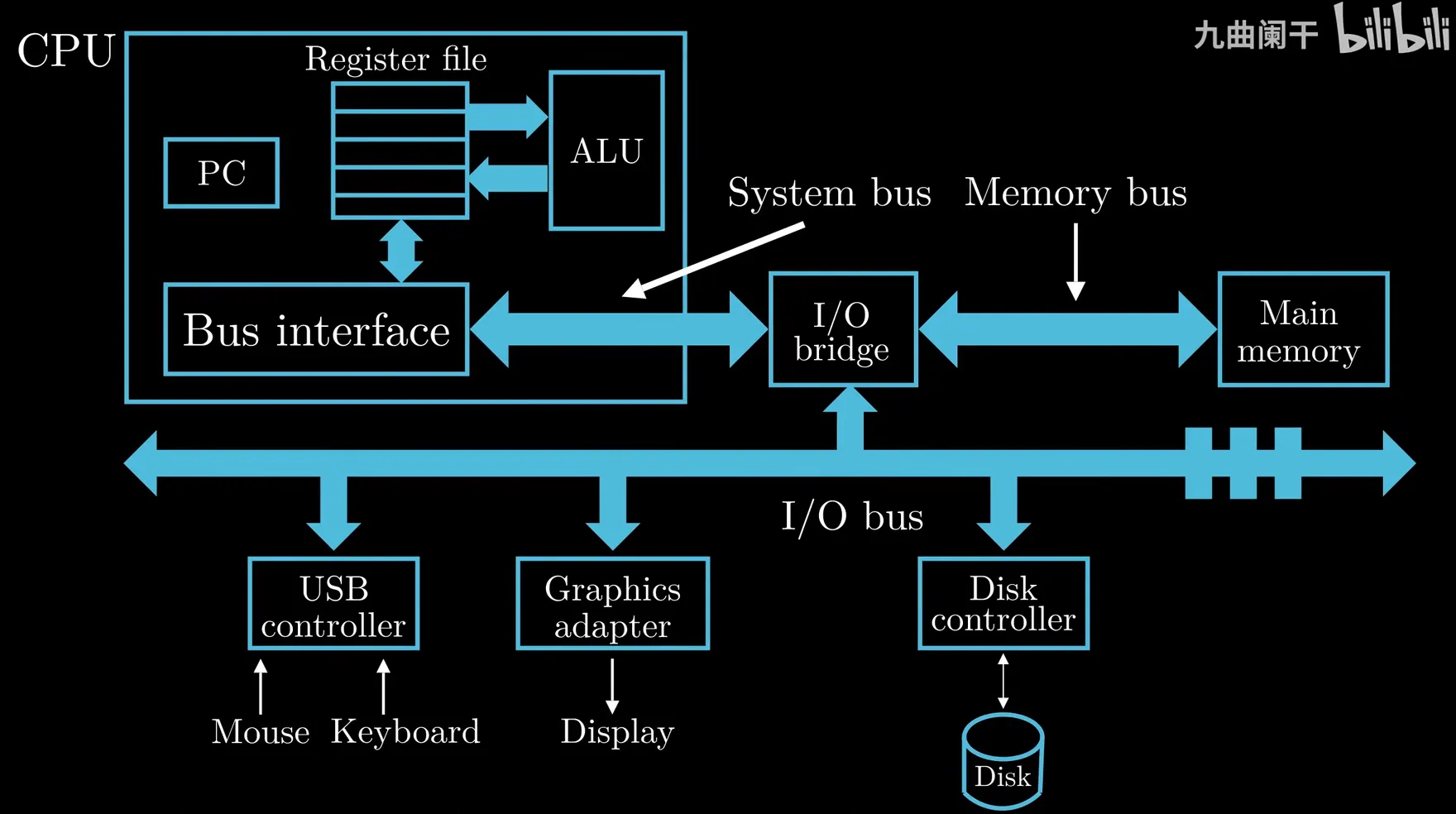 input by keyboard
input by keyboard
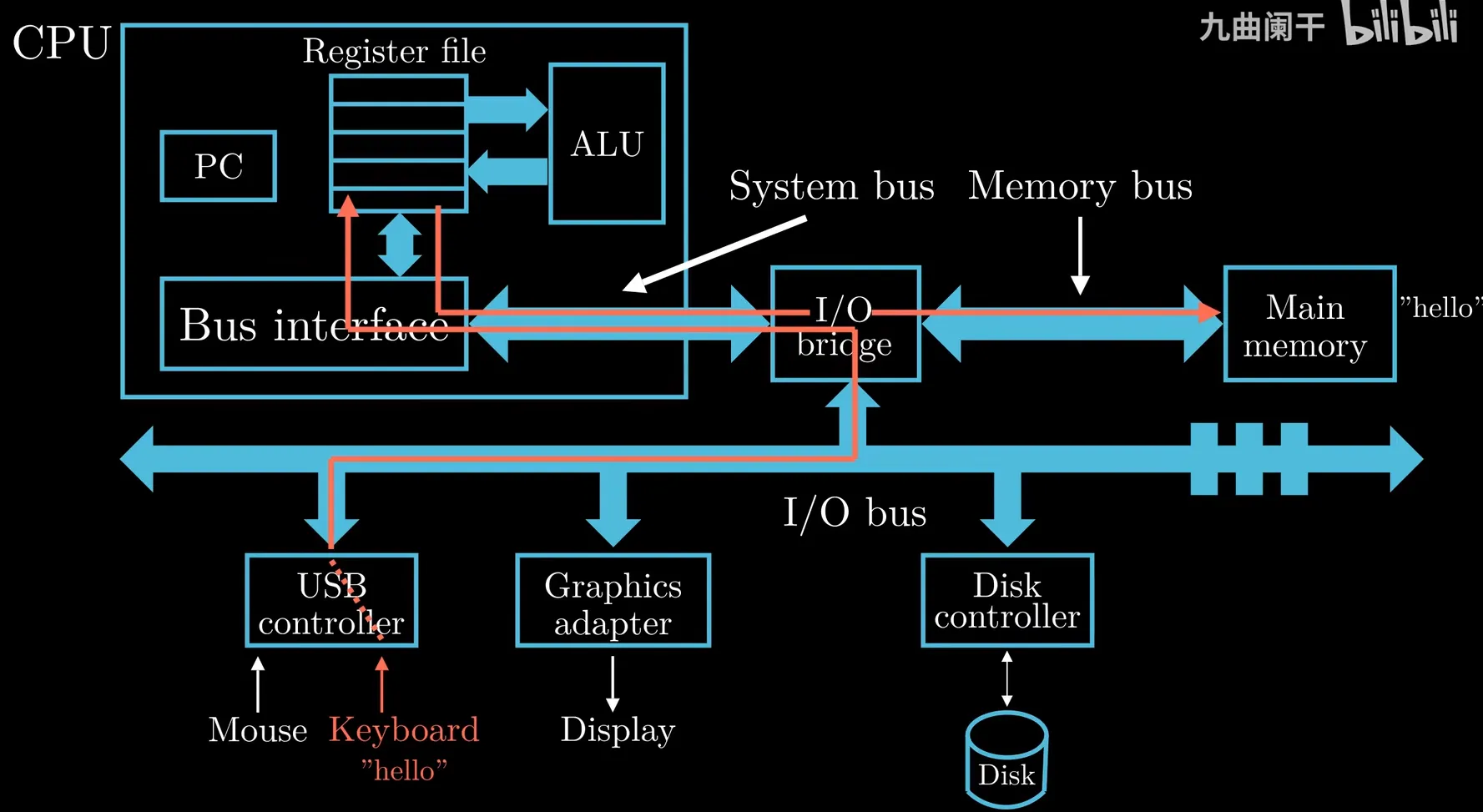 execution
execution
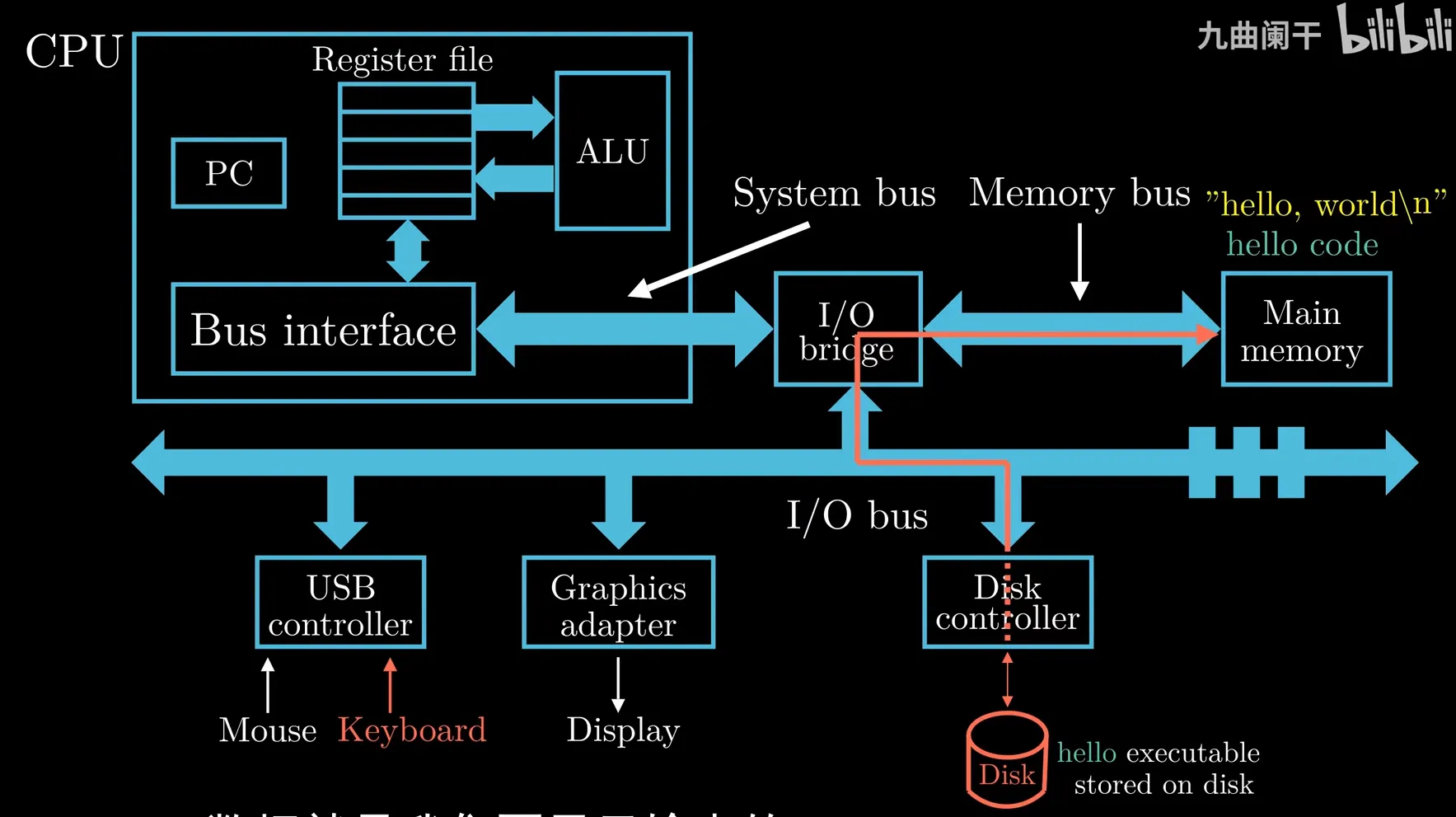 output through graphic
output through graphic
 {:height=“50%” width=“50%“}
{:height=“50%” width=“50%“} - large -> slow and cheap,
small -> fast and cost
上级层级是下级层级的高速缓存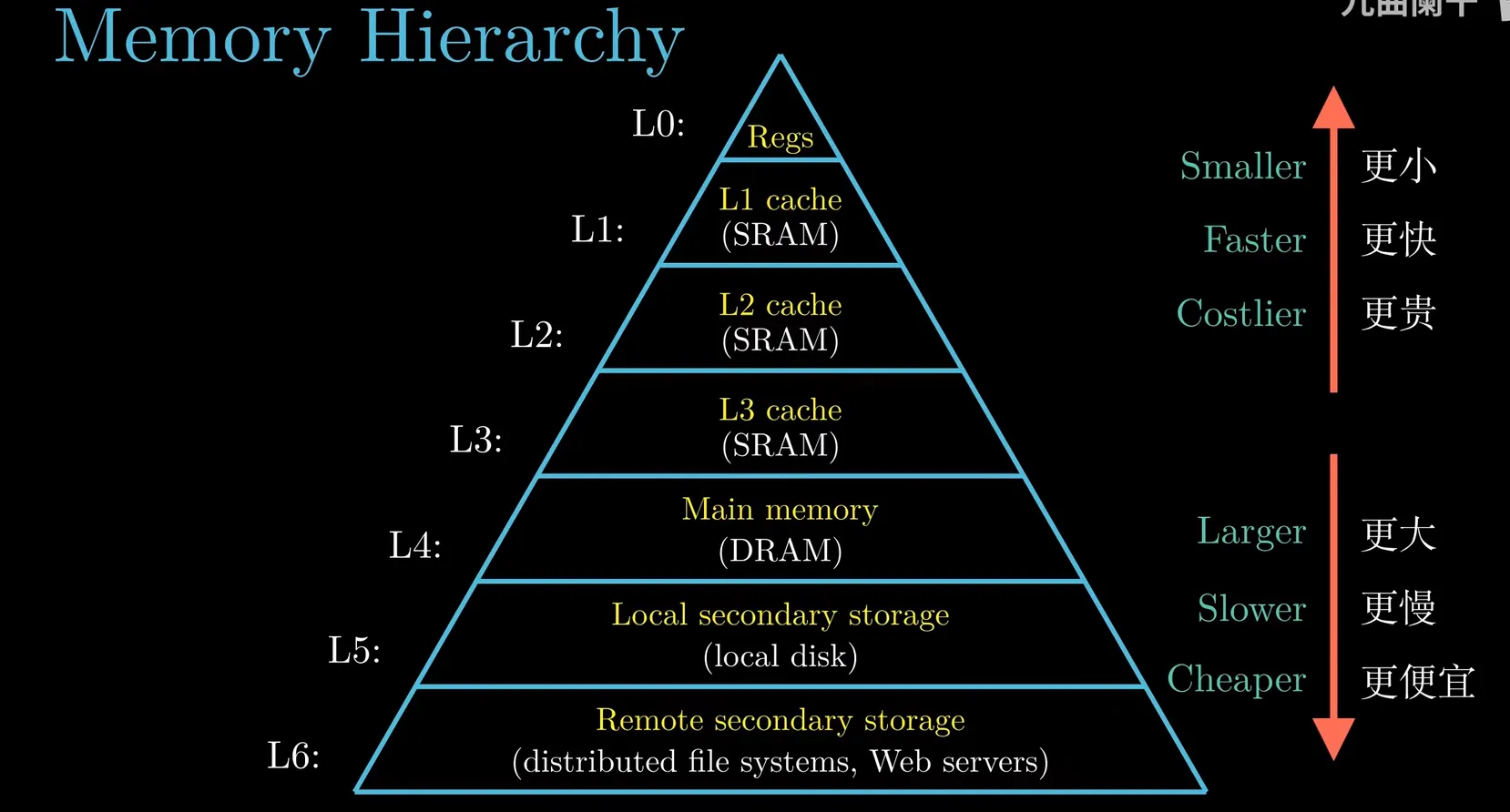 {:height=“50%” width=“50%“}
{:height=“50%” width=“50%“}
How to dramatically improve computer performance
Amdahl’s law s = 1 / ((1 - a) + a / k)
which indicate we need to work a lot if we want to improve computer’s performance.
-
Multi-core Processor(多核) : every CPU core has its L1 cache and L2 cache, all the cores share L3 cache.
-
Hyperthreading(超线程) : Instruction-Level Parallelism(流水线作业) Single Instruction Multiple Data
2. Representing and Manipulating Information
Information Storage
- Hexadecimal: start with
0x - Decimal
- Binary
- the storage of different types
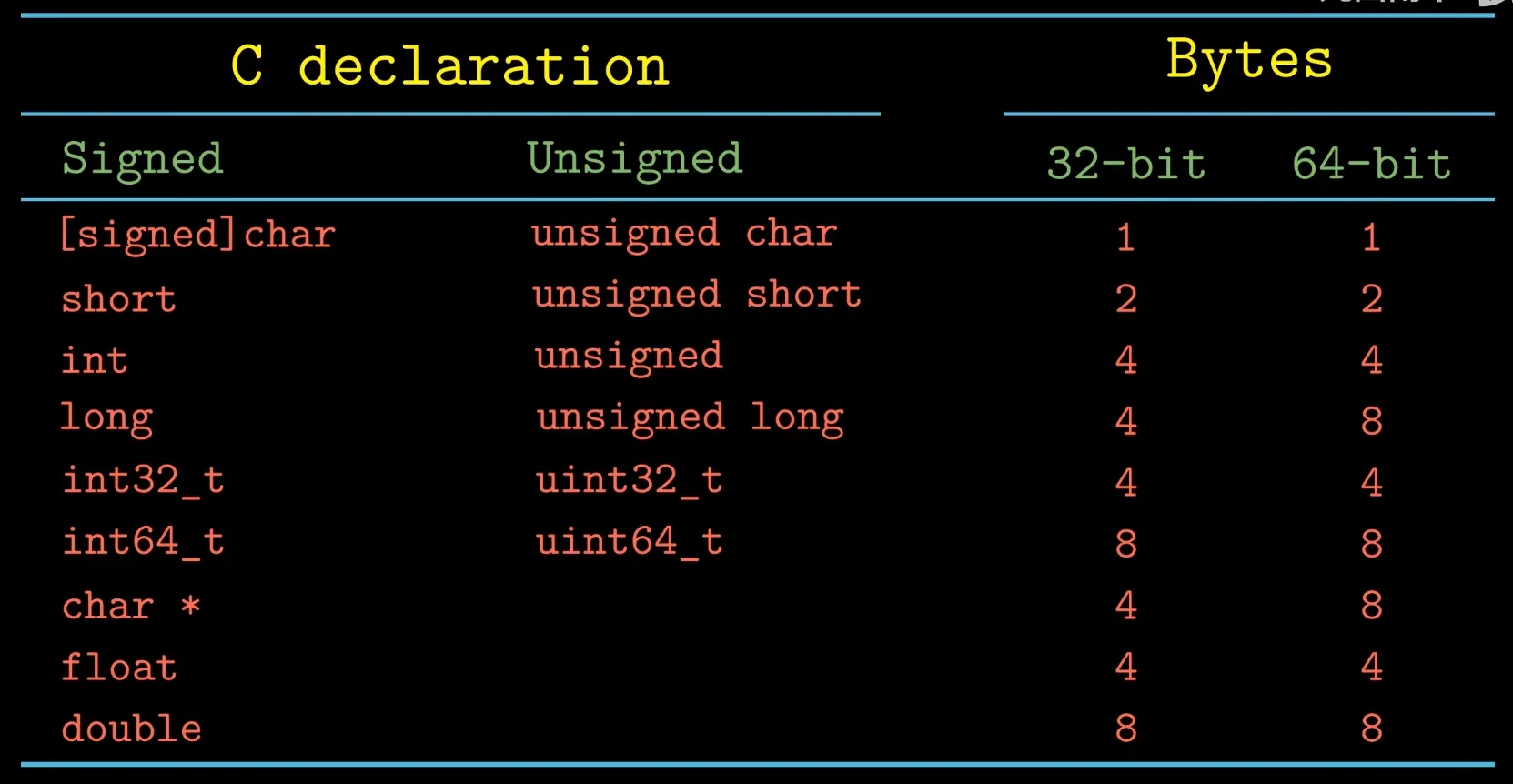
- Addressing and Byte Ordering: mostly machines use
Litlle Endian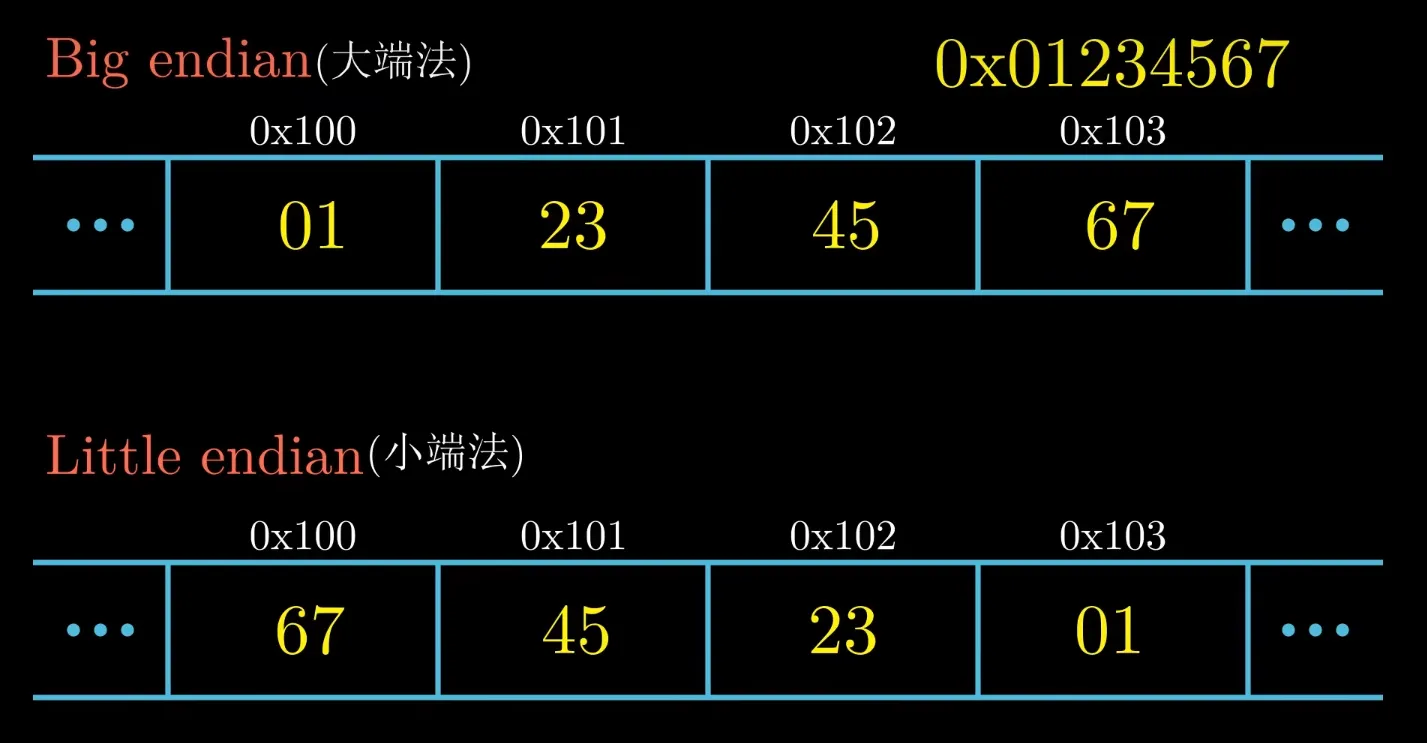
Integer Representations
Representation of negatives
-
Reverse Encoding(反码) : 1’ s complement: flip every single bit
: 负数是正数二进制按位取反的结果
shortcoming: error in representation of 0 -
Complement Encoding(补码) : 2’ s complement: flip every single bit and plus 1 : 最高位权重取负,其余与非负数表示相同。(最高位为1并不仅仅是取负号)
如1011 = -1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 -
Bias complement(偏码) : 比较大小时类似unsigned,同位时直接比较大小,实际值为表达式值加上bias值
bias = -(2 ^ (n-1) - 1)
Integer Arithmetic
if Overflow
- unsigned number: if
x + y > 2^w,x + y = x + y - 2^w - number:
- positive if
x + y > 2^w,x + y = x + y - 2^(w+1) - negative if
x + y < 2^w,x + y = x + y + 2^(w+1)
- positive if
Floating Point
- For normalized floats:
Value = (−1)^Sign ∗ 2^(Exp+Bias) ∗ 1.significand(2)- For denormalized(exponent all 0 and significand not all 0) floats:
Value = (−1)^Sign ∗ 2^(Exp+Bias+1) ∗ 0.significand(2)- Why exp need to be always 0? Cuz denorm is used to represent the numbers around 0.
-
float (32bit = 4Byte)
- sign 符号位 1bit (31): (-1)^n. 0 -> p, 1 -> n.
- exponent 指数位 8bit (30 - 23):
unsigned[0, 255] - bias(
(2 ^ (n-1) - 1)= 127)
scope: [-126, 127] (why not [-127, 128], 0000_0000, 1111_1111 represent infinite or NaN)
e.g. 1000_0001: (2^8 + 2^0) - 127- significand 小数位 23bit (22 - 0):
for normal float: 1 is implicit, so there is 24 bit actually
store as big endian: e.g.0100_0000...0000 = 2 ^ (-2)
-
double (64bit = 8Byte)
- sign 1bit (63)
- exponent 11bit (62 - 52)
- significand 53bit (52 - 0)
-
representation
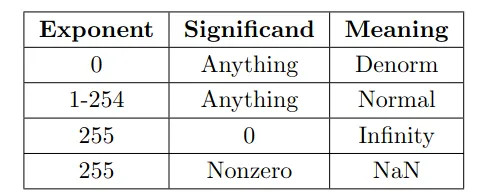
- +0: sign = 0, e = s = 0000_0000
- -0: sign = 1, e = s = 0000_0000
- +infinity: sign = 0, e = 1111_1111, s = 0000_0000
- -infinity: sign = 1, e = 1111_1111, s = 0000_0000
- NaN(Not a Number): sign = 0/1, e = 1111_1111, s != 0
-
transform
e.g. (10.75)10 to float
- represent as binary:
1010.11- Write binary numbers as 1.xxxx forms of scientific records:
1.01011*10^3- exponent + bias:
3+127 = 130so the exponent bit is1000_0010- significand:
0101_1000_0000_0000_0000_000- signal bit:
0, for 10.75 is positive- get result:
10.75 = 0|1000_0010|0101_1000_0000_0000_0000_000